


This past weekend was host to Ghost in the Shellcode 2015, an incredible CTF run by the excellent people in Men in Black Hats and Marauders. The team I play for, Samurai, ended up placing 2nd.
Of special note this year was Pwnadventure — an MMORPG which served as the foundation for 6 of the year’s challenges.
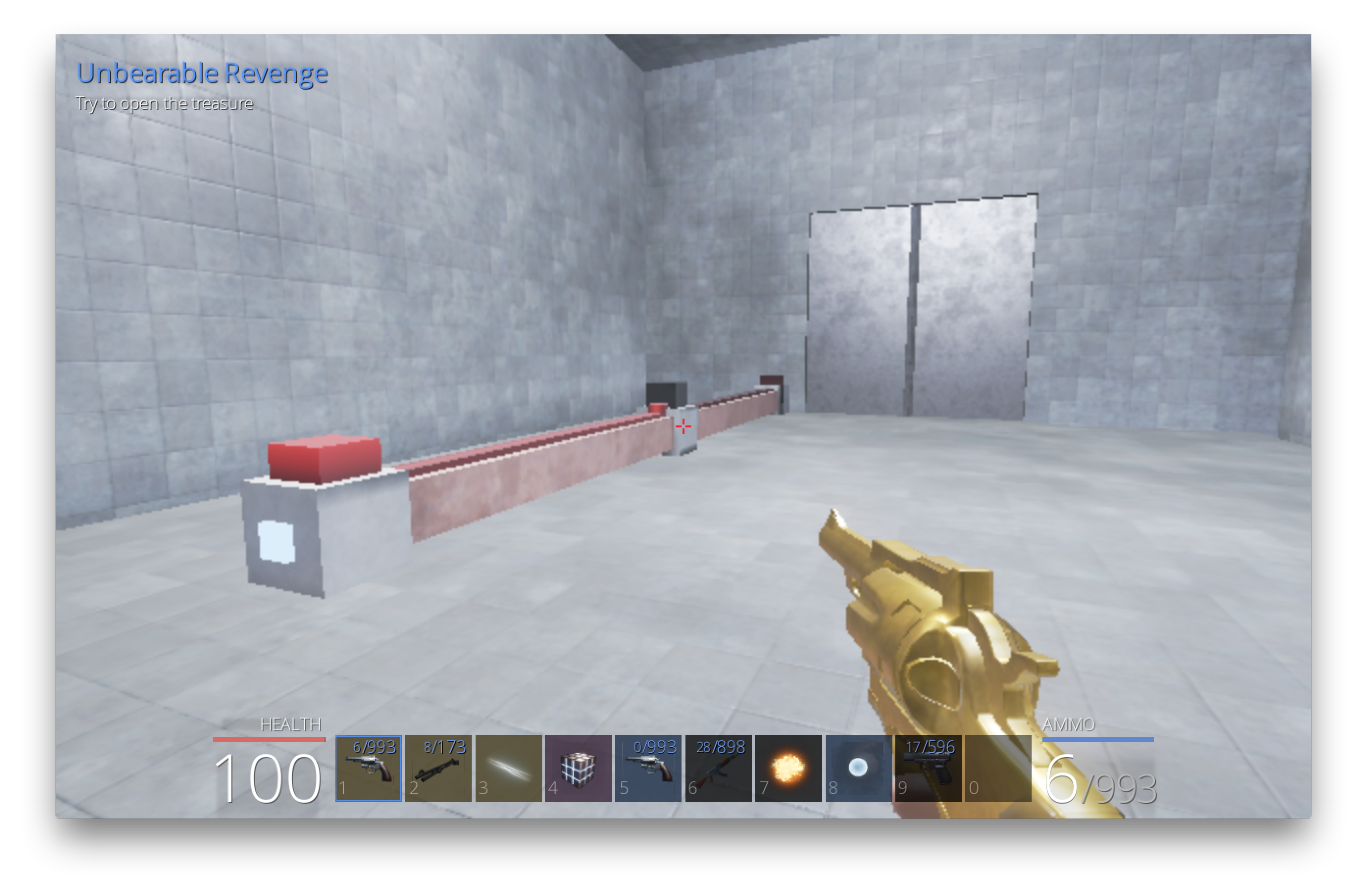
One of the challenges was Blocky’s Revenge, a reverse engineering problem I solved with my brilliant teammate Fugi. You started the challenge by finding “Fort Blox” hidden in one of the game’s many mountain ranges. At the entrance of the fort, was a room, pictured below, with a switch, two wires, a gate, and a locked door. It quickly became clear that the gate was a NOT gate, and that the door could be opened by simply flipping the switch off:
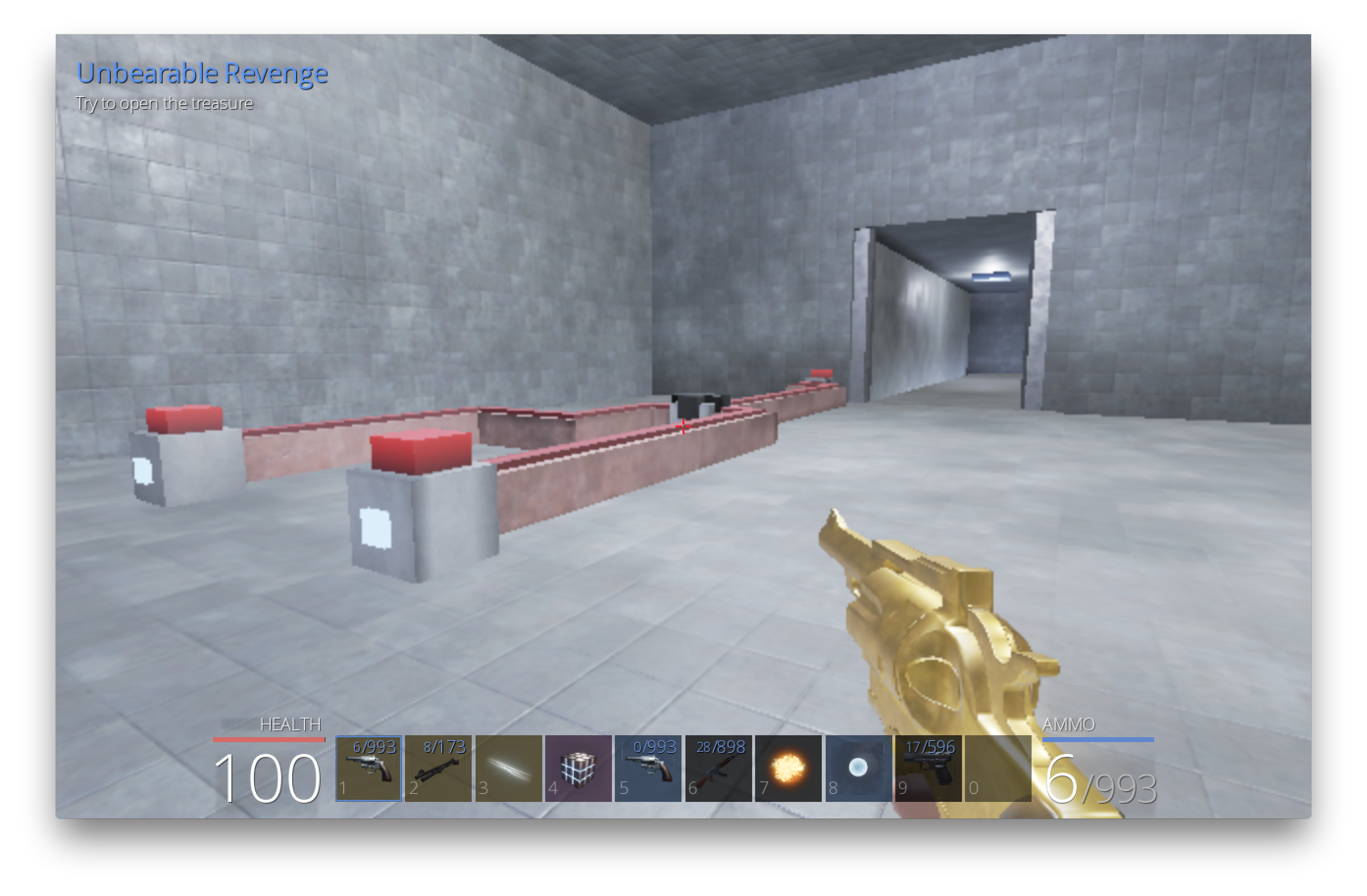
The next room contained an AND gate:
The following two rooms introduced us to OR gates and XOR gates. These rooms weren’t meant to pose a challenge, and instead simply served to introduce us to the rules behind the circuits. The fifth room was where things got difficult:

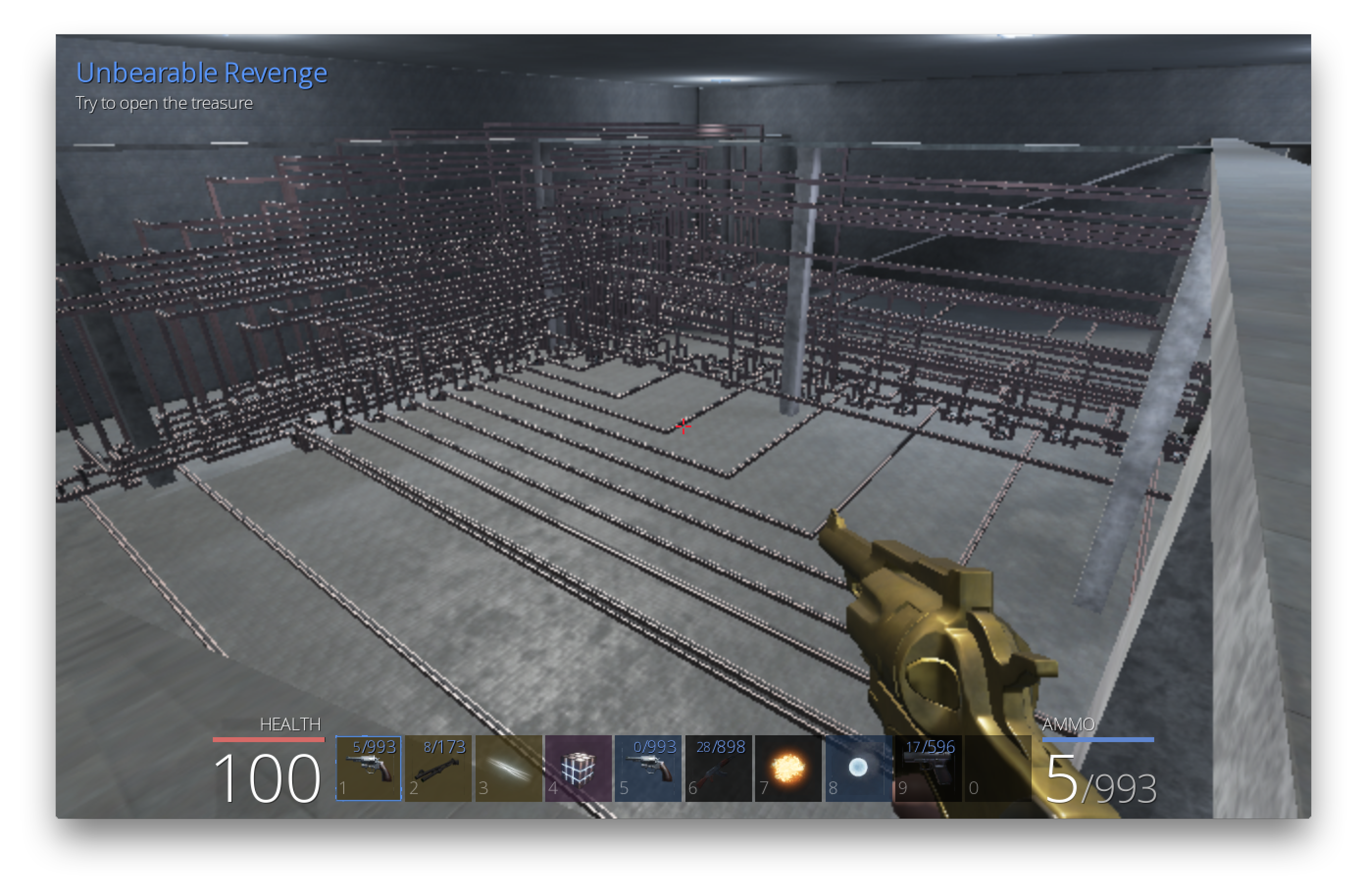
With a locked door at the far end of the room, and 32 switches at the entrance, it was clear that we were essentially looking at a combination lock, and had to find the arrangement of switches that would unlock the door.
Fugi and myself set to work on transcribing the circuit to paper, so that we could more easily have a feel for what we were looking at. We split the circuit in half, and set to work on migrating it to a Google Docs spreadsheet. After a few hours, we were done.
The circuit contained 40 rows, each with anywhere between 2 and 42 gates.
The spreadsheet gave us a great medium for experimenting with the circuit, while also seeing all of the intermediate state. Try copying the spreadsheet into your own document and modifying the values in the “switch” column to see what we mean.
With 2^32 possibilities, we weren’t prepared to try them all. Instead, realizing that the circuit encoded a boolean formula, and that we were being asked to produce a model that satisfies the formula, we turned to Z3, a theorem prover developed by Microsoft Research.
We used our spreadsheet to define a formula within Z3, then used Z3 to prove satisfiability and produce a model.
Running Z3 — try it yourself online — gives the following model:
(declare-const c2 Bool)
(declare-const c3 Bool)
(declare-const c4 Bool)
(declare-const c5 Bool)
(declare-const c6 Bool)
(declare-const c7 Bool)
(declare-const c8 Bool)
(declare-const c9 Bool)
(declare-const c10 Bool)
(declare-const c11 Bool)
(declare-const c12 Bool)
(declare-const c13 Bool)
(declare-const c14 Bool)
(declare-const c15 Bool)
(declare-const c16 Bool)
(declare-const c17 Bool)
(declare-const c18 Bool)
(declare-const c19 Bool)
(declare-const c20 Bool)
(declare-const c21 Bool)
(declare-const c22 Bool)
(declare-const c23 Bool)
(declare-const c24 Bool)
(declare-const c25 Bool)
(declare-const c26 Bool)
(declare-const c27 Bool)
(declare-const c28 Bool)
(declare-const c29 Bool)
(declare-const c30 Bool)
(declare-const c31 Bool)
(declare-const c32 Bool)
(declare-const c33 Bool)
(define-fun f2 () Bool (not c18))
(define-fun f3 () Bool (not c20))
(define-fun f4 () Bool (not c4))
(define-fun f5 () Bool (not c22))
(define-fun f6 () Bool (not c6))
(define-fun f7 () Bool (not c24))
(define-fun f8 () Bool (not c26))
(define-fun f9 () Bool (not c10))
(define-fun f10 () Bool (and c7 c26))
(define-fun f11 () Bool (not c28))
(define-fun f12 () Bool (xor c7 c27))
(define-fun f13 () Bool (not c8))
(define-fun f14 () Bool (not c27))
(define-fun f15 () Bool (not c30))
(define-fun f16 () Bool (and c10 c29))
(define-fun f17 () Bool (not c9))
(define-fun f18 () Bool (not c28))
(define-fun f19 () Bool (not c14))
(define-fun f20 () Bool (and c11 c30))
(define-fun f21 () Bool (xor c10 c29))
(define-fun f22 () Bool (not c32))
(define-fun f23 () Bool (xor c11 c30))
(define-fun f24 () Bool (not c16))
(define-fun f25 () Bool (xor c13 c32))
(define-fun f26 () Bool (xor c15 c18))
(define-fun f27 () Bool (not c6))
(define-fun f28 () Bool (not c25))
(define-fun f29 () Bool (not c5))
(define-fun f30 () Bool (not c24))
(define-fun f31 () Bool (not c4))
(define-fun f32 () Bool (not c23))
(define-fun f33 () Bool (not c3))
(define-fun f34 () Bool (not c22))
(define-fun f35 () Bool (not c2))
(define-fun f36 () Bool (not c17))
(define-fun f37 () Bool (not c20))
(define-fun f38 () Bool (not c16))
(define-fun f39 () Bool (not c19))
(define-fun f40 () Bool (and c15 c18))
(define-fun f41 () Bool (not c14))
(define-fun f42 () Bool (and c13 c32))
(define-fun f43 () Bool (not c12))
(define-fun i2 () Bool (not f12))
(define-fun i3 () Bool (and f17 f18))
(define-fun i4 () Bool (xor f13 f14))
(define-fun i5 () Bool (xor f17 f18))
(define-fun i6 () Bool (and c31 f43))
(define-fun i7 () Bool (xor c33 f41))
(define-fun i8 () Bool (xor f38 f39))
(define-fun i9 () Bool (xor f36 f37))
(define-fun i10 () Bool (xor c21 f35))
(define-fun i11 () Bool (xor f34 f33))
(define-fun i12 () Bool (xor f31 f32))
(define-fun i13 () Bool (xor f29 f30))
(define-fun i14 () Bool (xor f27 f28))
(define-fun i15 () Bool (and f27 f28))
(define-fun i16 () Bool (and f29 f30))
(define-fun i17 () Bool (and f31 f32))
(define-fun i18 () Bool (and f33 f34))
(define-fun i19 () Bool (and f35 c21))
(define-fun i20 () Bool (and f36 f37))
(define-fun i21 () Bool (and f38 f39))
(define-fun i22 () Bool (and f41 c33))
(define-fun i23 () Bool (xor c31 f43))
(define-fun l2 () Bool (xor i14 f10))
(define-fun l3 () Bool (or i2 f11))
(define-fun l4 () Bool (and c26 c7 i14))
(define-fun o2 () Bool (or l2 f9))
(define-fun o3 () Bool (or i15 l4))
(define-fun r2 () Bool (xor i13 o3))
(define-fun r3 () Bool (and o3 i13))
(define-fun u2 () Bool (not r2))
(define-fun u3 () Bool (or i16 r3))
(define-fun x2 () Bool (xor i12 u3))
(define-fun x3 () Bool (or u2 f8))
(define-fun x4 () Bool (and u3 i12))
(define-fun aa2 () Bool (not x2))
(define-fun aa3 () Bool (or i17 x4))
(define-fun ad2 () Bool (xor i11 aa3))
(define-fun ad3 () Bool (or aa2 c8))
(define-fun ad4 () Bool (and aa3 i11))
(define-fun ag2 () Bool (or ad2 f7))
(define-fun ag3 () Bool (or i18 ad4))
(define-fun aj2 () Bool (xor i10 ag3))
(define-fun aj3 () Bool (and ag3 i10))
(define-fun am2 () Bool (not aj2))
(define-fun am3 () Bool (or i19 aj3))
(define-fun l8 () Bool (xor i9 am3))
(define-fun l9 () Bool (or am2 f6))
(define-fun l10 () Bool (and am3 i9))
(define-fun o8 () Bool (or l8 f5))
(define-fun o9 () Bool (or i20 l10))
(define-fun r8 () Bool (xor i8 o9))
(define-fun r9 () Bool (and o9 i8))
(define-fun u8 () Bool (not r8))
(define-fun u9 () Bool (or i21 r9))
(define-fun x8 () Bool (xor f26 u9))
(define-fun x9 () Bool (or u8 f4))
(define-fun x10 () Bool (and u9 f26))
(define-fun aa8 () Bool (or x8 f3))
(define-fun aa9 () Bool (or f40 x10))
(define-fun ad8 () Bool (xor i7 aa9))
(define-fun ad9 () Bool (and aa9 i7))
(define-fun ag8 () Bool (not ad8))
(define-fun ag9 () Bool (or i22 ad9))
(define-fun aj8 () Bool (xor f25 ag9))
(define-fun aj9 () Bool (or ag8 c2))
(define-fun aj10 () Bool (and ag9 f25))
(define-fun am8 () Bool (not aj8))
(define-fun am9 () Bool (or f42 aj10))
(define-fun l13 () Bool (or am8 f2))
(define-fun l14 () Bool (and am9 i23))
(define-fun l15 () Bool (xor i23 am9))
(define-fun o13 () Bool (or i6 l14))
(define-fun o14 () Bool (not l15))
(define-fun r13 () Bool (and o13 f23))
(define-fun r14 () Bool (xor f23 o13))
(define-fun u13 () Bool (or f20 r13))
(define-fun u14 () Bool (not r14))
(define-fun x13 () Bool (and u13 f21))
(define-fun x14 () Bool (xor f21 u13))
(define-fun x15 () Bool (or u14 f22))
(define-fun aa13 () Bool (or f16 x13))
(define-fun aa14 () Bool (or x14 f19))
(define-fun aa15 () Bool (or o14 f24 x15))
(define-fun ad13 () Bool (and aa13 i5))
(define-fun ad14 () Bool (xor i5 aa13))
(define-fun ag13 () Bool (or i3 ad13))
(define-fun ag14 () Bool (not ad14))
(define-fun aj13 () Bool (xor i4 ag13))
(define-fun aj14 () Bool (or ag14 f15))
(define-fun am13 () Bool (not aj13))
(define-fun am14 () Bool (or aa15 aa14 aj14))
(define-fun l21 () Bool (or am13 c12))
(define-fun o21 () Bool (or am14 l21 l3))
(define-fun r21 () Bool (or o21 o2 x3))
(define-fun u21 () Bool (or r21 ad3 ag2))
(define-fun x21 () Bool (or u21 l9 o8))
(define-fun aa21 () Bool (or x21 x9 aa8))
(define-fun ad21 () Bool (or aa21 aj9 l13))
(define-fun ag21 () Bool (not ad21))
(assert ag21)
(check-sat)
(get-model)Which encodes the solution: 01101001100011111010101111111010
By returning to the game and flipping the switches to their respective positions, the door opens, and the challenge is completed.